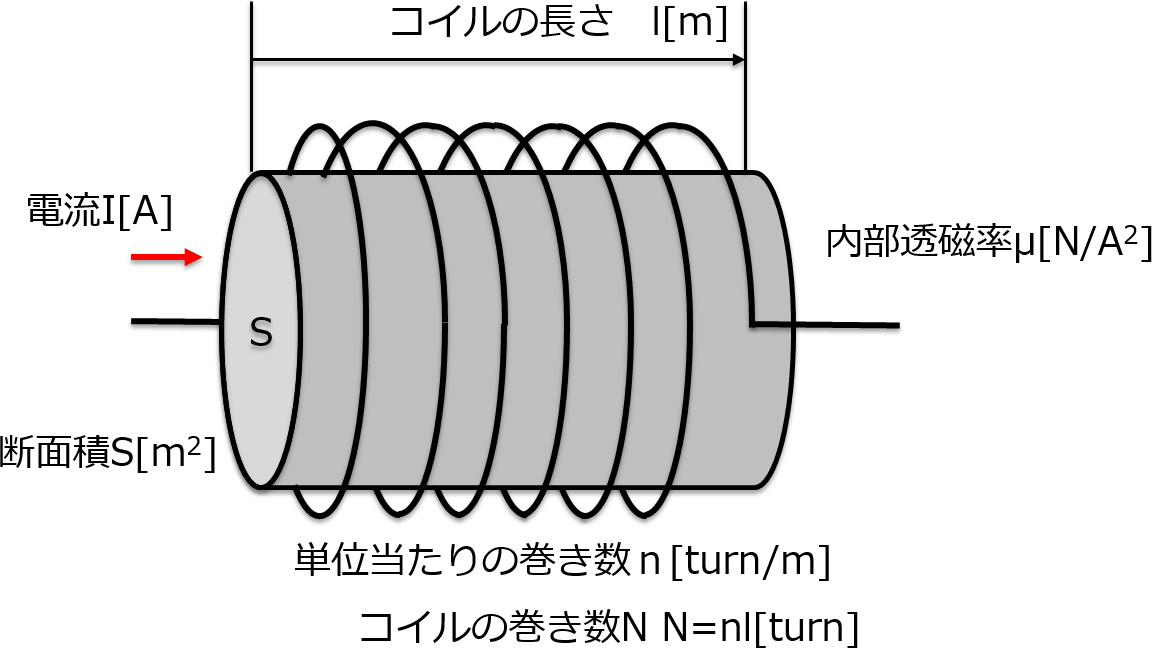
誘導起電力の比 物理範囲 1次コイル、2次コイルに流れる電流をそれぞれ I1e A * 、 I2e A とし、発生する誘導起電力をそれぞれ V1e V 、 V2e V とし、コイルの巻き数をそれぞれ N1 、 N2 とし、コイルを貫く磁束を Φ Wb とします。 は交流電源のマークです。 電源の電圧を V0e V とし3 コイルの太さや巻き数は ・ コイルの作る磁界は単位長さ当たりの巻き数に比例し,電流に比例する。 従って,密に巻くほど,電流を流すほど磁界は強くなる。 ・ したがって,電気抵抗がなければ,コイルは密に,たくさん巻くに越したことはない。 できるだけ1か所にまとめて巻く方がよい。 ・ 現実的には,導線に電気抵抗があり,導線が太いほど電流は流れ デュアルコイル (コイル二つ)のRDAを使用します。 シングルで03Ωはほとんどやりません、私の場合。 という事は06Ωを二つ付ければオッケー でここから先はアトマ次第でゲージ
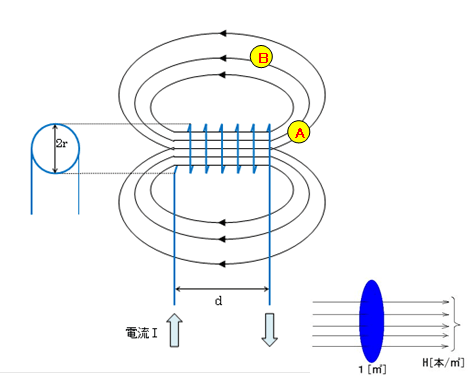
磁気の話 磁界h と磁束f 電流 I と巻数 N Electric
コイル 公式 巻き数
コイル 公式 巻き数-インダクタ編 No1「インダクタ(コイル)の基礎知識①」 過去の記事を整理・一部リライトして再掲載したものです。 古い技術情報や、 現在、TDKで扱っていない製品情報なども含まれています図2 は,2つのコイルと1つのコアからなる理想トランスのイメージ図です.コイルは導線を巻いたインダクタですが,ここではコイルと呼ぶことにします. 図2 は,左側のコイルを1次側,右側のコ




変圧器と交流送電 大学受験の王道
2コイルの巻き数について コイルを作るとき、どれぐらいの長さのコイル を作ればソレノイドになるのかについて調べたの が右の図のグラフである。直径18cmの塩化ビニ ルパイプに直径045mmコイル部の端から端までの全巻数、押しバネは両端の座を引いた有効巻数が計算(設計)で必要 total number of coils 押しばね (圧縮)の場合は、端から端までの座も含めたすべて数えたのを総巻数または、全巻数と呼びその確認の仕方は通常、目視で行ないます、設計記号はNt。 この種類に関しては次の項で解説の有効Naや座巻きと区別し確認、指定をします。 押し電磁石 (でんじしゃく、electromagnet)は通常、磁性材料の芯のまわりに、 コイル を巻き、通電することによって一時的に磁力を発生させる 磁石 である。 機械要素として用いられる。 電流を止
= コイルの中心軸上の間隔(メートル) しかし、実際のコイルは複数回巻かれているので、磁場を作るために流れる全電流は = total current となる。ここで、 = 片側のコイルのワイヤの巻き数 を※コイルの形状(どちらか選択&入力) 円形 長方形 コイルの直径 mm コイルの幅 mm コイルの高さ mm ※計算モード(どちらか選択&入力) インダクタンスから巻き数を計算 巻き数からイン100回巻きのコイル。 そして、0回巻きのコイルです。 それぞれのコイルに、かん電池を一個ずつつないで、くっつくくぎの数を比かくしてみましょう。 50回巻きでは、このくらい。 100回巻



トロイダルコア 内部磁束 平均磁路長 コアの断面積 コイルの巻き数 コイルに流す電流 コアの透磁率 1アマの無線工学 R02年09月期 A 02




変圧器と交流送電 大学受験の王道



Q Tbn And9gcq Lrs1m0edmtlrdnytxss62ixmx5vzb3wh86xhziy Npnxklftr0ud Usqp Cau



相互インダクタンス 自己インダクタンス 合成インダクタンス 磁気的な結合 結合係数 相互の磁力線の向き トロイダルコア 1アマの無線工学 H11年04月期 A 04




コイルの自己誘導 高校物理をあきらめる前に 高校物理をあきらめる前に




電流が作る磁界の強さ やさしい電気回路
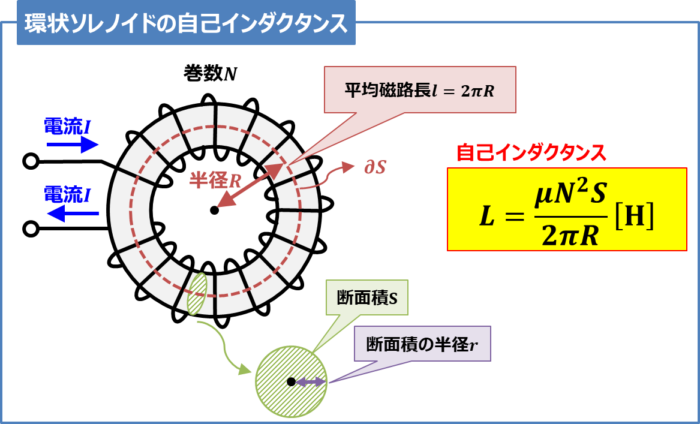



環状ソレノイドの自己インダクタンス 公式 と 導出方法 について
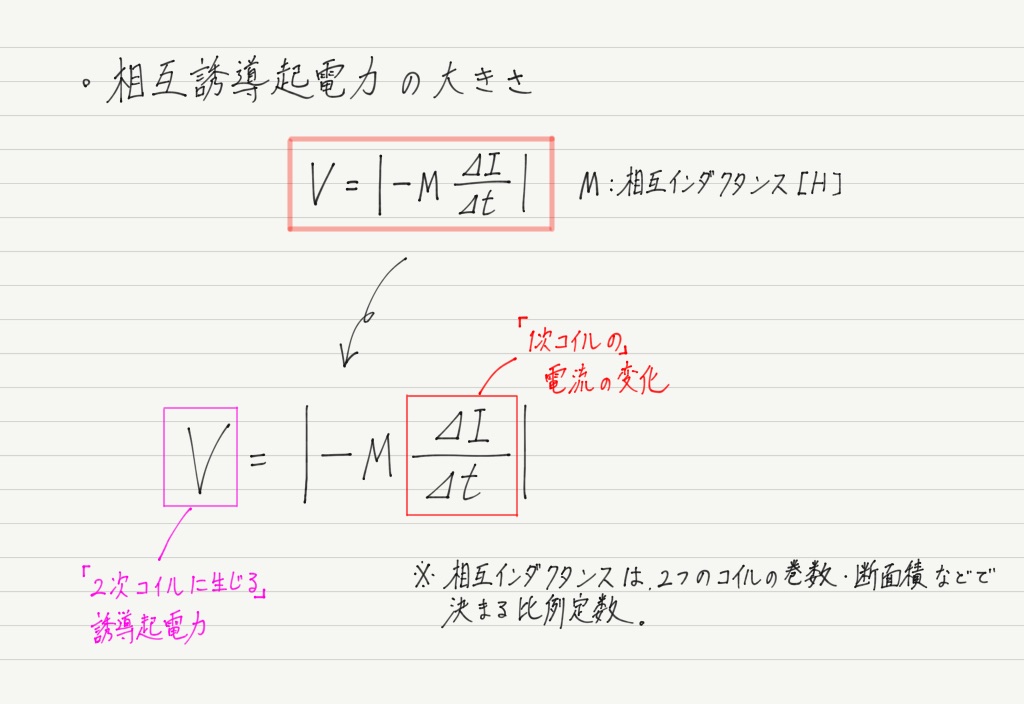



コイルの相互誘導 高校物理をあきらめる前に 高校物理をあきらめる前に




変圧器 わかりやすい高校物理の部屋



Q Tbn And9gcrwcfw5afj27qjp5wpgq68xoqmch2ifcdmu6gqkjjzzed Zu1pv4oqh Usqp Cau



コイルの設計 巻線仕様を計算する ソレノイドコイル ヘルムホルツコイル 日本ユニバーサル電気株式会社



電気回路 その4



電磁気 電磁誘導




コイルと磁界の強さ 電験3種 理論 最速合格




高校物理 変圧の仕組み 自己誘導と相互誘導 電磁気 お茶処やまと屋




2
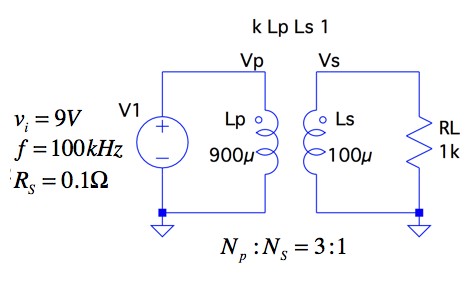



トランスの巻き数と入力 出力電圧の関係 Cq出版社 オンライン サポート サイト Cq Connect
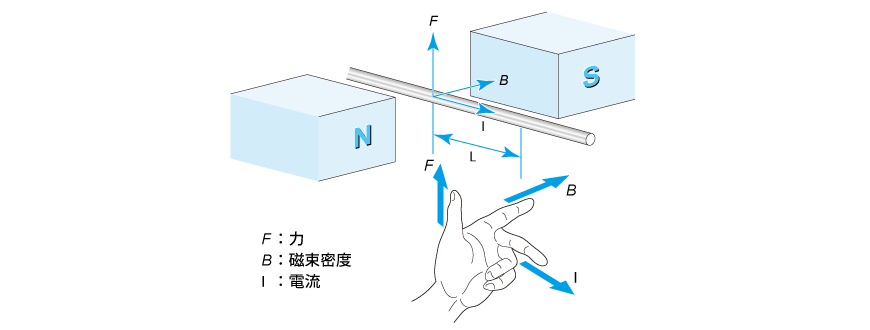



2 1 2 回転原理の基礎 日本電産株式会社



電気回路 その4
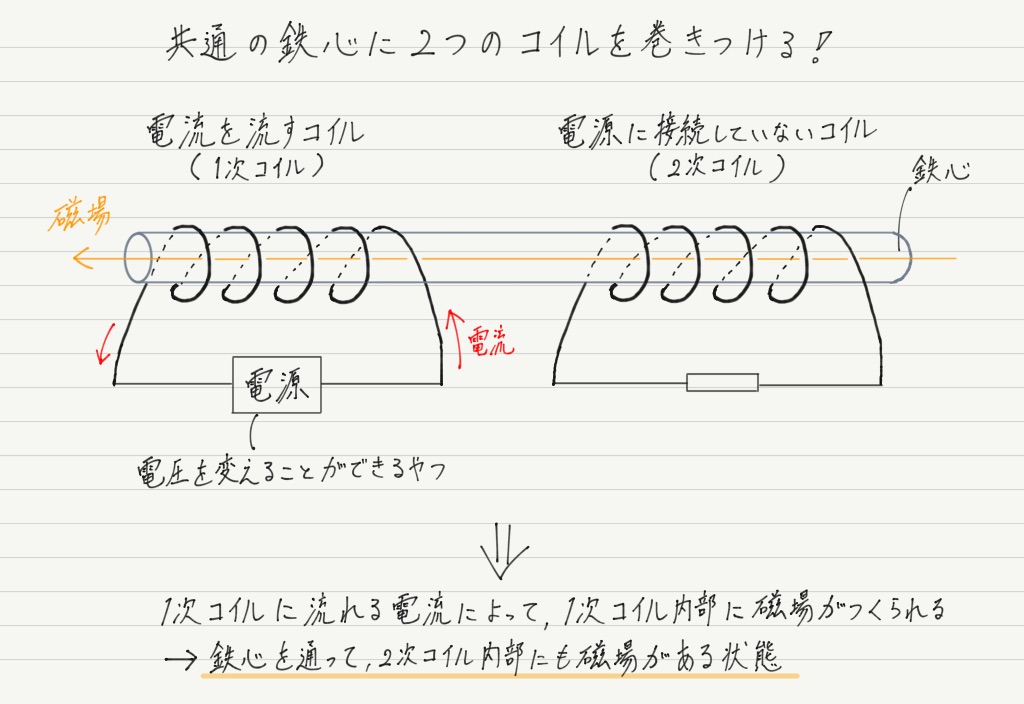



コイルの相互誘導 高校物理をあきらめる前に 高校物理をあきらめる前に



コイルの巻数の計算 コイル内部の磁界の計算 この問題の式が分か Yahoo 知恵袋




高校物理 変圧器 Youtube




ファラデーの電磁誘導の法則 高校物理をあきらめる前に 高校物理をあきらめる前に




高校物理 変圧の仕組み 自己誘導と相互誘導 電磁気 お茶処やまと屋
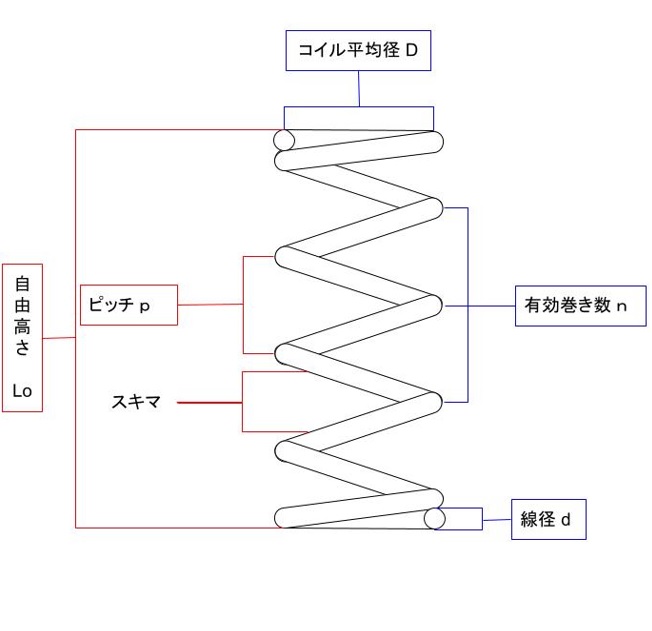



圧縮コイルばねの計算 ばねの総合メーカー フセハツ工業株式会社
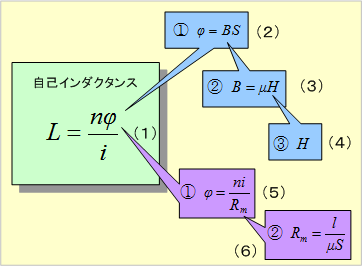



インダクタンス物語 5 インダクタンスの求め方 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会



コイルの種類と時定数を学ぶ Aps 組み込み業界専門メディア



トロイダルコア 内部磁束 平均磁路長 コアの断面積 コイルの巻き数 コイルに流す電流 コアの透磁率 1アマの無線工学 R02年09月期 A 02



コイルの巻き数を増やすと 5年 電磁石の性質 かたりつづけていきます



コイル 自己インダクタンス 棒状の物質 リアクタンス 電流と電圧の位相 透磁率 巻き数 1アマの無線工学 H17年08月期 A 01




磁気回路 やさしい電気回路




過去15年で出た ソレノイドコイル の相互インダクタンスを求める問題3 Physicmath フィジクマス




電気工事士1種 コイルの巻線に電流が流れたときの鉄心内に生じる磁束 H26年度問1 ふくラボ電気工事士



Jo1pct Amateur Radio Station
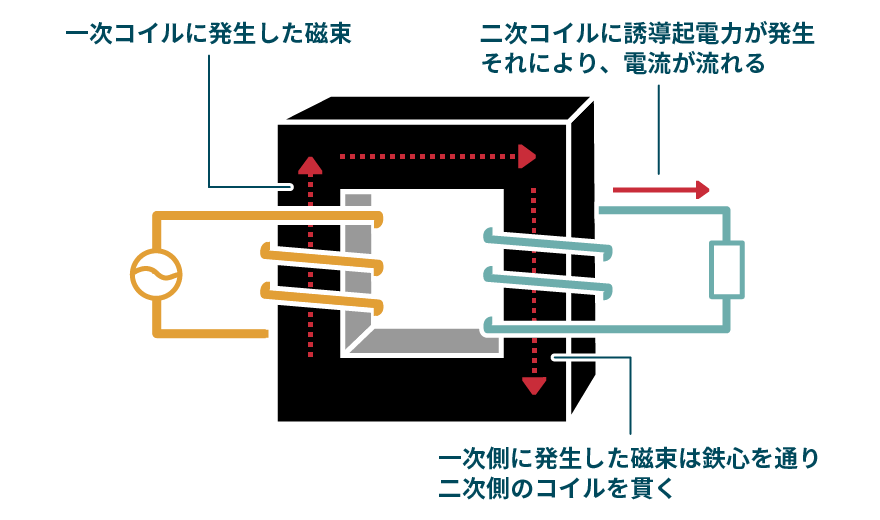



変圧器とは 原理や構造をわかりやすく解説 Technology Geeks 株式会社ダイヘン
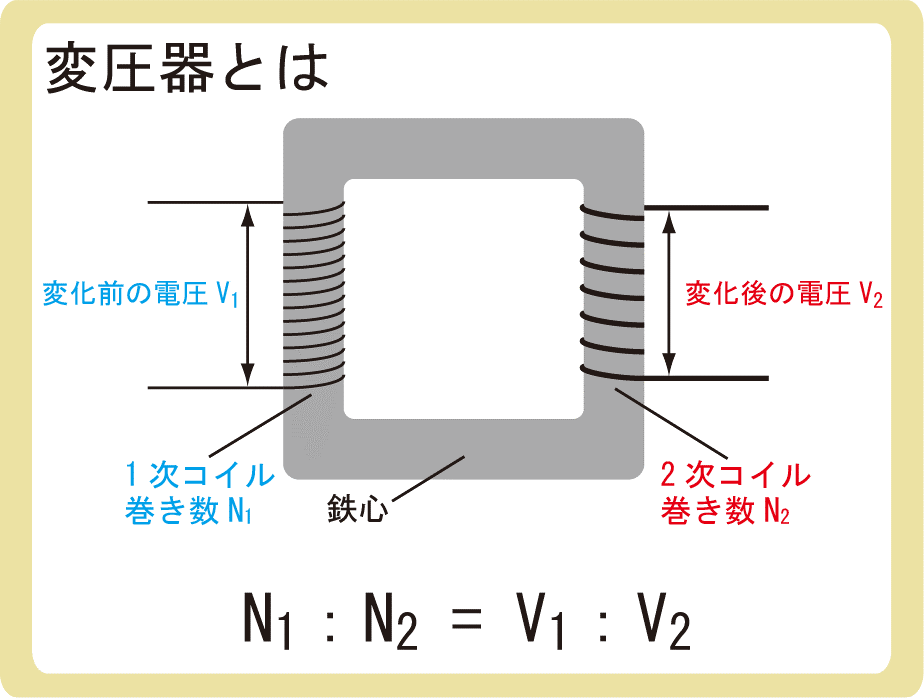



変圧器とは 送電について ぷち教養主義



磁場の持つエネルギーと電流を担う電荷が持つ運動エネルギー
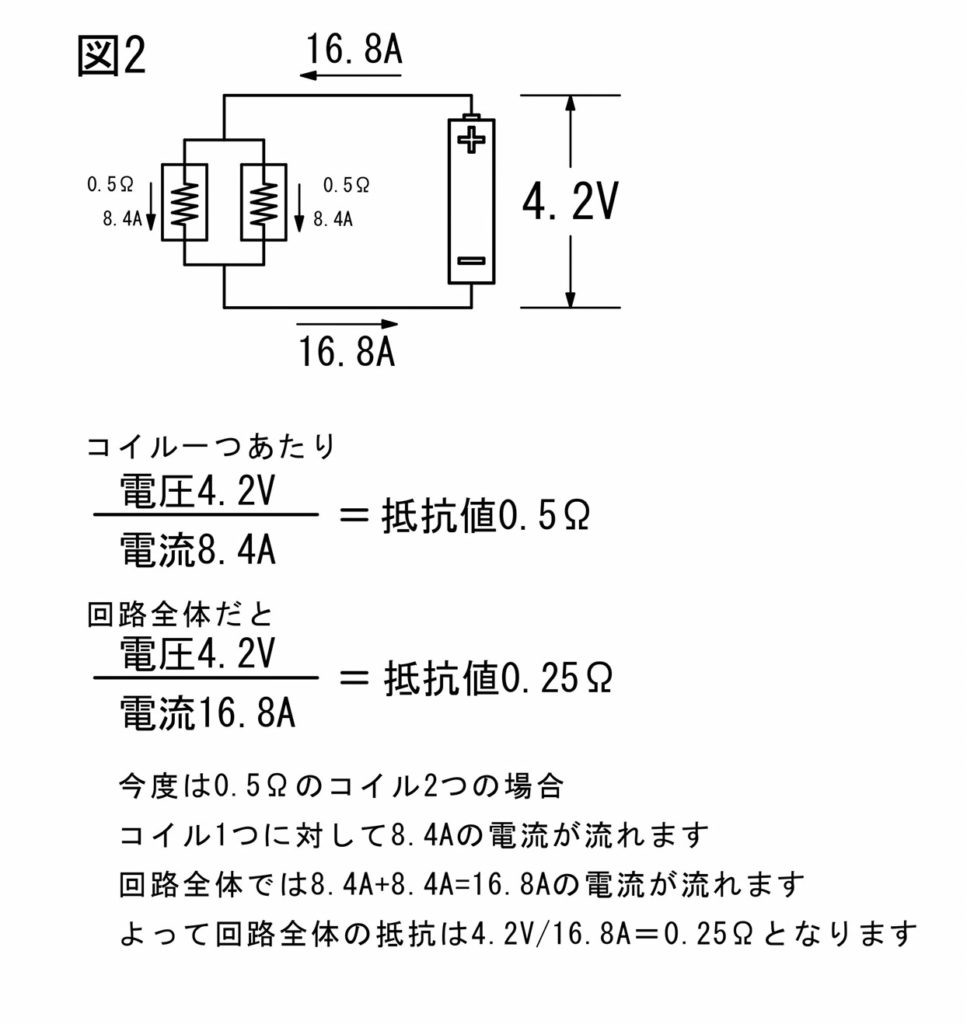



コイルの抵抗 ワイヤーの選定 巻き数の決定等々のお話 ベイホク店長岡野の場合 Vape北海道 公式サイト




過去15年で出た ソレノイドコイル の相互インダクタンスを求める問題1 Physicmath フィジクマス




理論磁気分野対策 電流が作る磁界 磁場 の公式と次元解析 エレペディア




ループコイルで粗密のあるコイルを扱う方法 磁場解析 ムラタソフトウェアブログ




Page8 コイルの巻き数アップで安定感のある12v化を実現 特集記事 バイクブロス
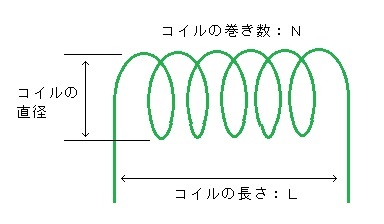



皆空の中で 測定器なしで空芯コイルのインダクタンスを調べる
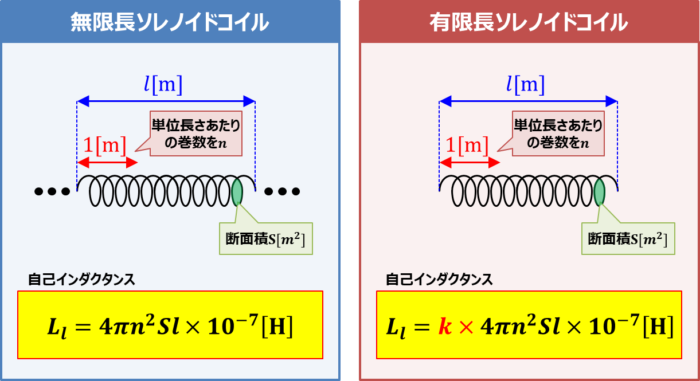



ソレノイドコイルの自己インダクタンス 公式 と 導出方法 について




磁気の話 磁界h と磁束f 電流 I と巻数 N Electric




コイルに使用する銅線の長さの計算
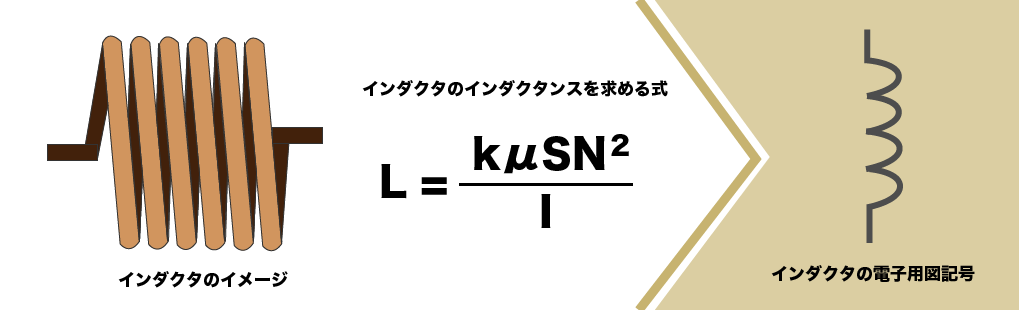



インダクタとは コイルとの違いはある 半導体 電子部品とは Corecontents コアスタッフ株式会社 Corecontents




皆空の中で 夏休みの工作 ゲルマ ラジオの製作




高校物理 変圧器 映像授業のtry It トライイット



ソレノイドコイルの簡単設計 長岡係数 インダクタンス 日本ユニバーサル電気株式会社
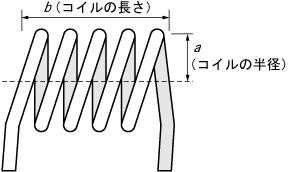



トランジスタ技術 エレクトロニクス数式集 オンライン計算シート 空芯コイルの巻き数と半径からインダクタンスを求める



ピックアップの基礎知識
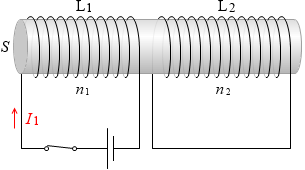



相互誘導 わかりやすい高校物理の部屋
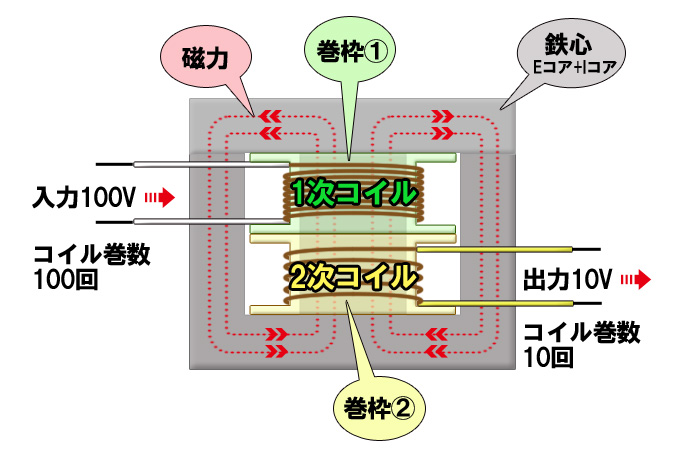



今さら聞けない 電源トランスのレギュレーションとは 過去メルマガ一覧 加美電子工業株式会社



ソレノイド コイル の設計 Scoilcalc




コンパコラム 4 磁束密度公式導出その2 Bw Physics Note




理論磁気分野対策 電流が作る磁界 磁場 の公式と次元解析 エレペディア



自己インダクタンスが巻き数の2乗に比例することについて良くわからな Yahoo 知恵袋




磁気回路 やさしい電気回路




電検三種 理論 磁気の重要ポイント ヘルニアクソ野郎エンジニアblog



2
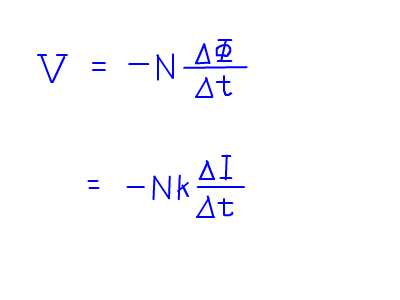



Return 15年02月
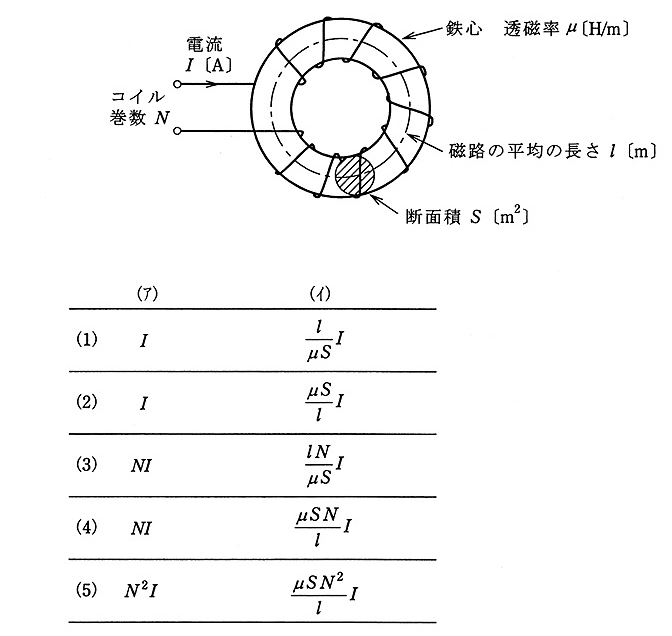



自己インダクタンス 基礎からわかる電気技術者の知識と資格



この電磁気学の問題を教えて下さい 図のように 断面積4 0 Yahoo 知恵袋
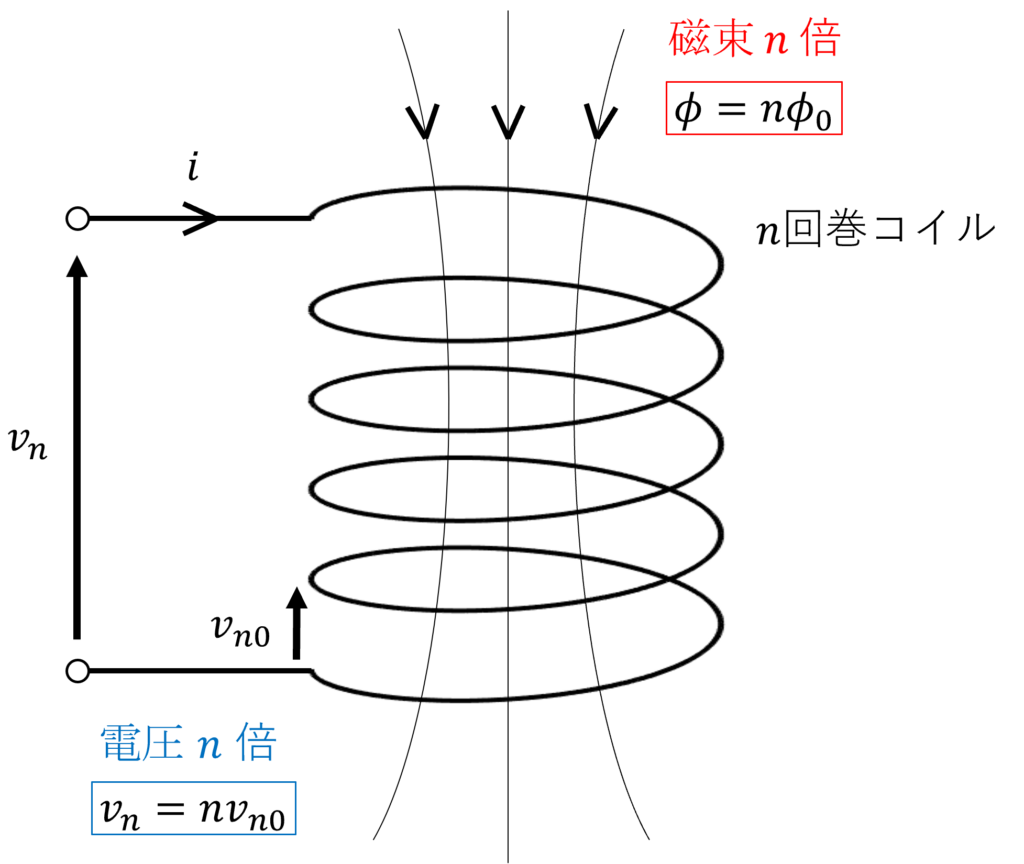



鎖交磁束と自己インダクタンス 電気回路 例題つき 大学の知識で学ぶ電気電子工学
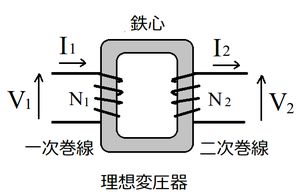



理想変圧器の原理 計算式




変圧器の原理 やさしい電気回路



Q Tbn And9gcr19xbis5azlpmlh1bhzrtpc2ziymqcckjm14moqgcq2dg3o8nnyuws Usqp Cau




トランス 変圧器の原理 Koko物理



コア入りソレノイド




電磁誘導 電磁気 公式 大学受験の王道




誘導起電力とは 公式や向きの求め方を理解するためのポイントを紹介 高校生向け受験応援メディア 受験のミカタ




空芯コイルの設計方法 Qucsstudio Emc村の民
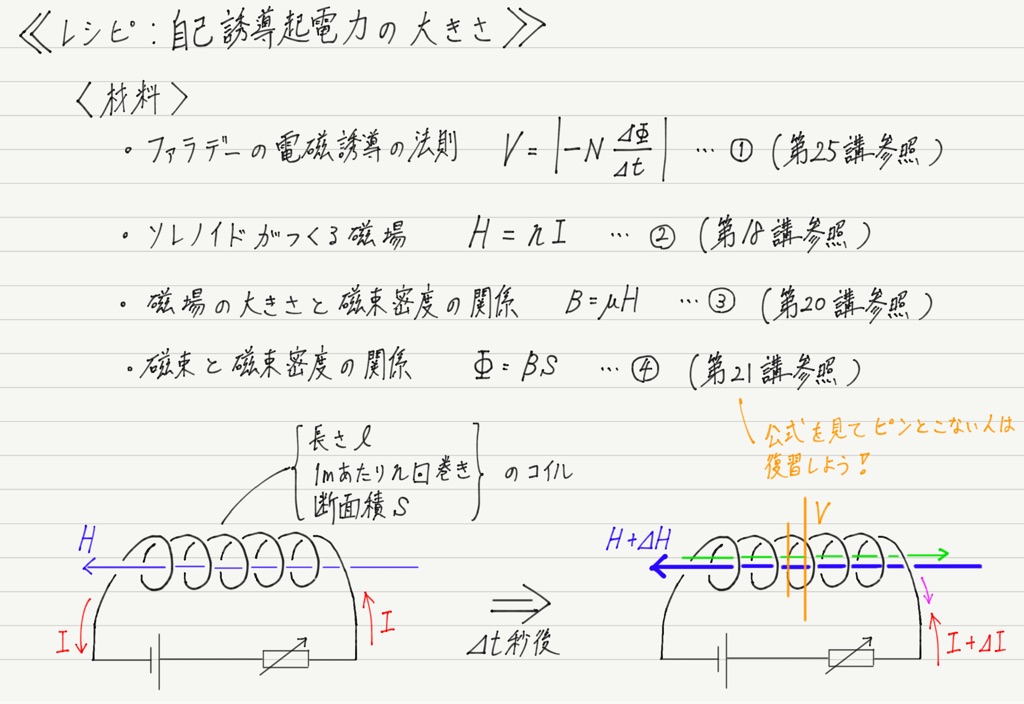



コイルの自己誘導 高校物理をあきらめる前に 高校物理をあきらめる前に




コイルビルド講座 22mmrtaシングルの場合 Vape 電子タバコ レビュー ブログ Smoky Vape Load



ソレノイドコイルの磁束密度 1 0 当たりの巻き数が40回であ Yahoo 知恵袋
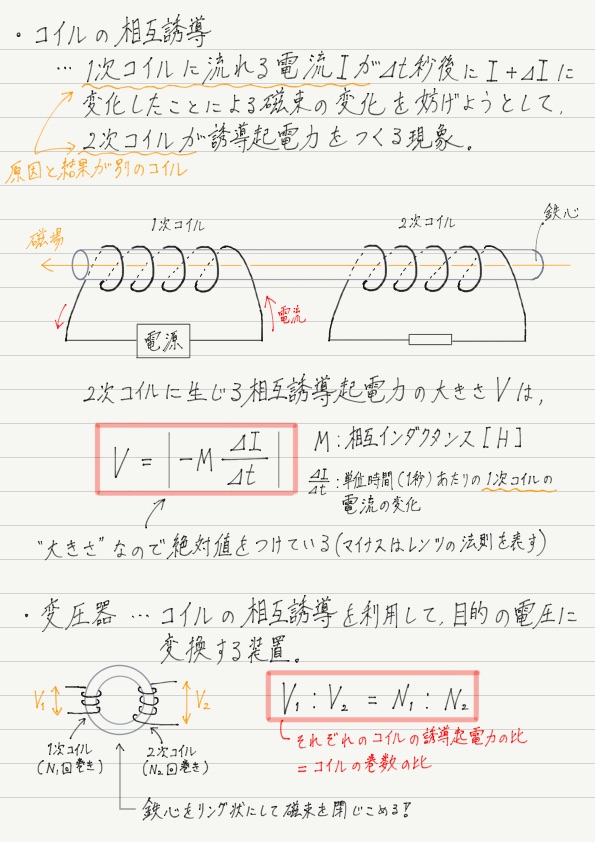



コイルの相互誘導 高校物理をあきらめる前に 高校物理をあきらめる前に



一辺がaメートル 巻き数nの正方形コイルが均一な誘磁界bの中で Yahoo 知恵袋
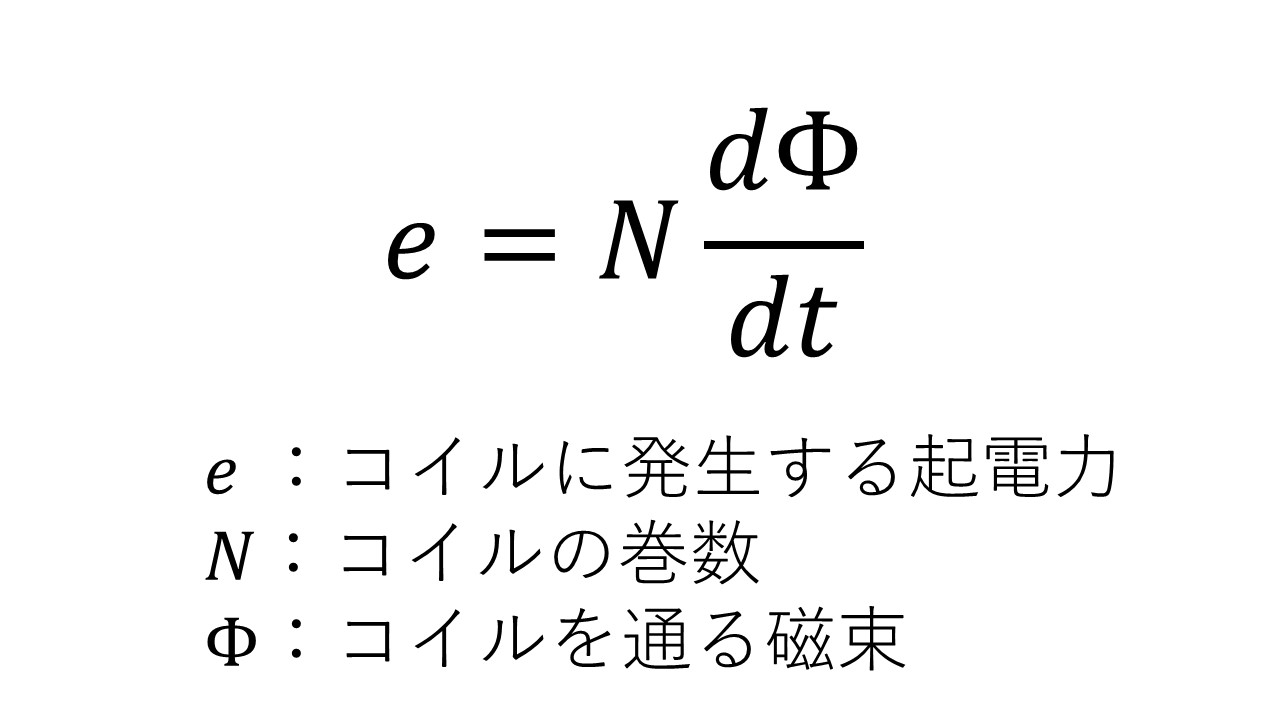



変圧器の原理を分かりやすく解説 ハヤシライスblog




高校物理 変圧の仕組み 自己誘導と相互誘導 電磁気 お茶処やまと屋
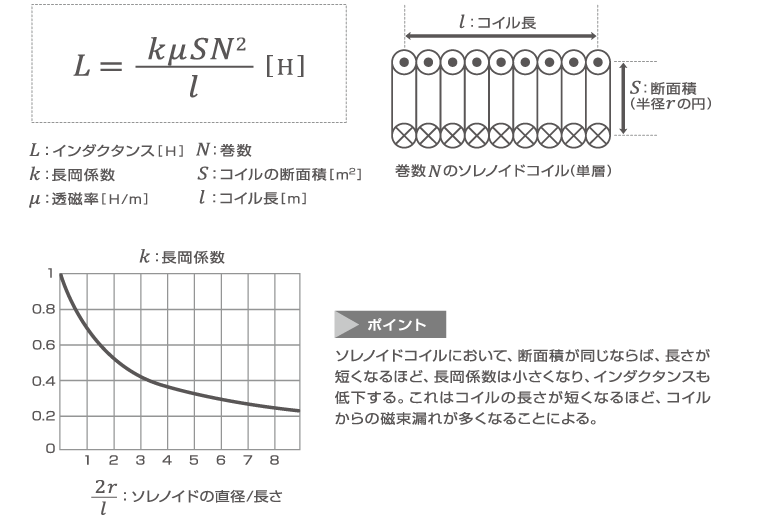



インダクタ コイル の基礎知識 エレクトロニクス入門 Tdk Techno Magazine




鎖交磁束と自己インダクタンス 電気回路 例題つき 大学の知識で学ぶ電気電子工学
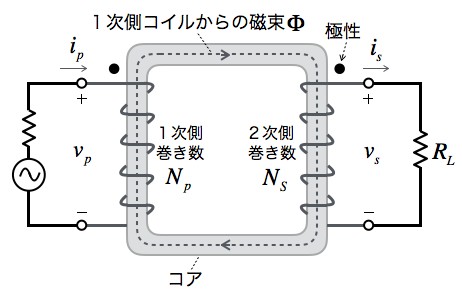



トランスの巻き数と入力 出力電圧の関係 Cq出版社 オンライン サポート サイト Cq Connect
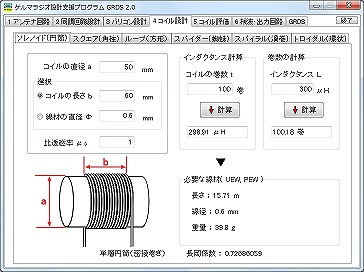



設計計算
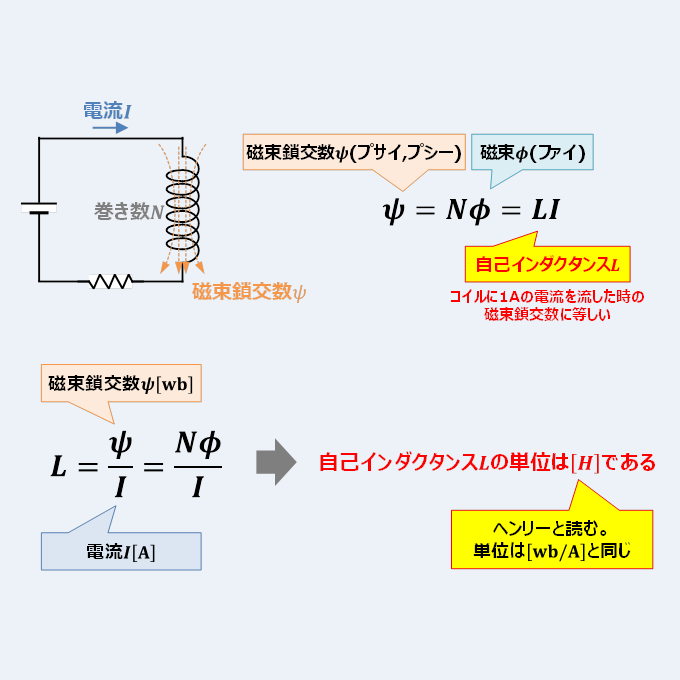



自己インダクタンスのまとめ 単位 や 問題 などを解説
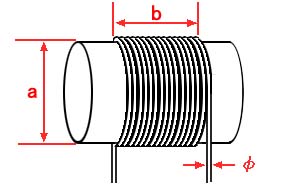



ソレノイドコイルの巻数とインダクタンス




マナ物理 自己誘導 その1 解説 自己誘導とは コイルに流れる電流が変化するとき コイル自身が作りだす磁場によって起電力が生じる現象 自己インダクタンスは コイルの巻き数 形状 内部の物質などで決まるコイル固有の物理量です それが



短縮コイルの計算 Jr1gdy 点と線をつないで Good Ham Life
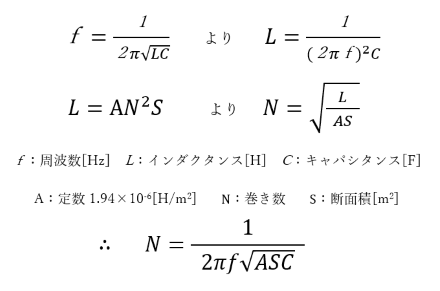



ループアンテナの巻き数
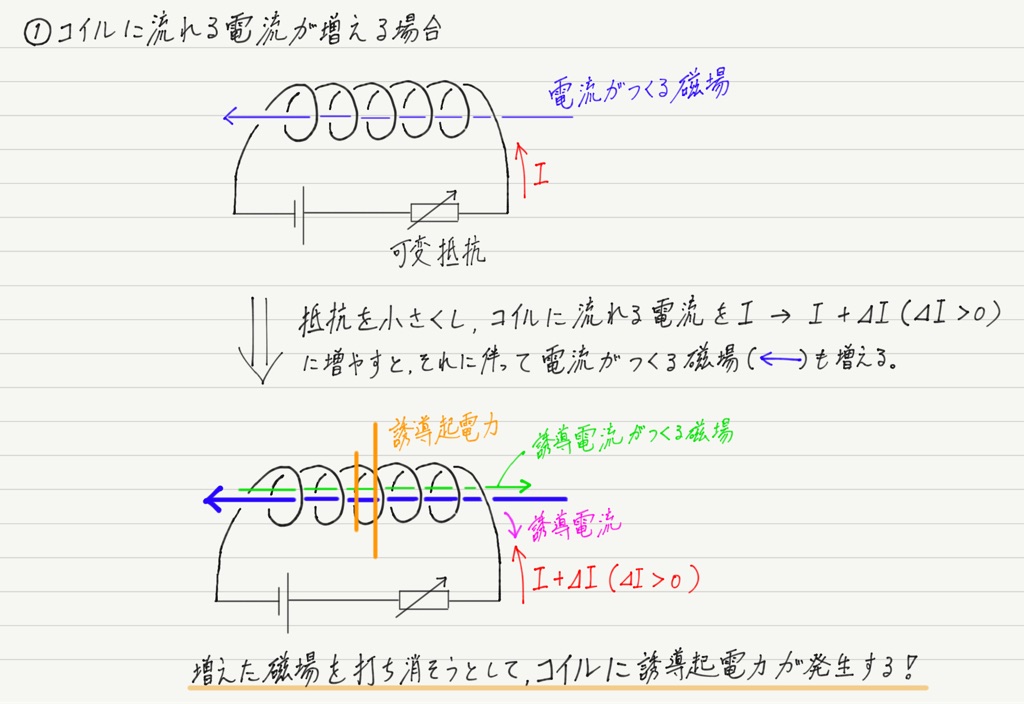



コイルの自己誘導 高校物理をあきらめる前に 高校物理をあきらめる前に



Imagehp006 Png




自己インダクタンスのまとめ 単位 や 問題 などを解説



Q Tbn And9gcs1svmpmrxdokkbcsjuumqsq6rejeigewcbwgr95wwdvu9wirstg Q3 Usqp Cau
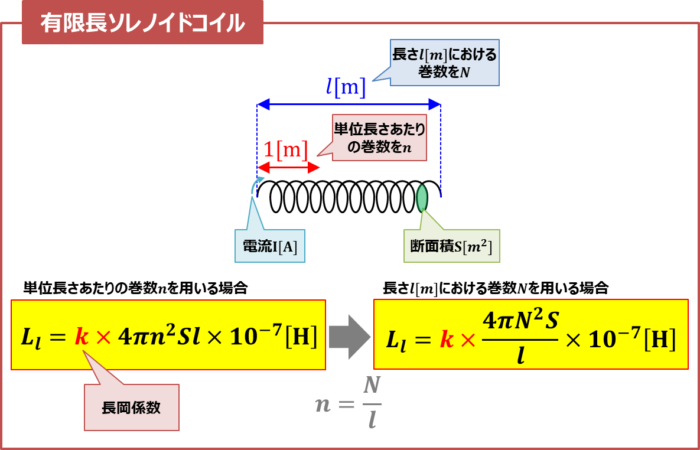



ソレノイドコイルの自己インダクタンス 公式 と 導出方法 について
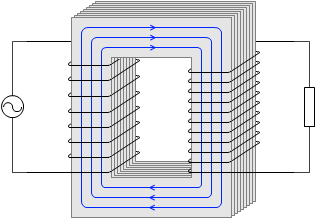



変圧器 わかりやすい高校物理の部屋




自作コイルの測定 追記あり ほよほよのブログ
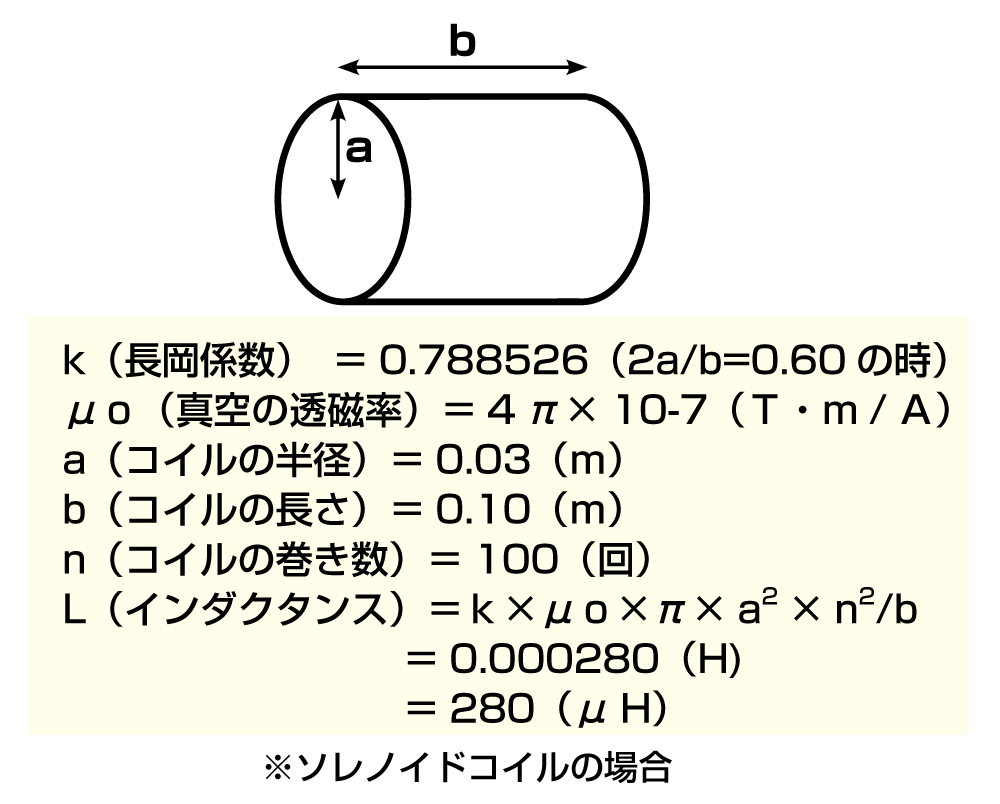



磁気式のワイヤレス給電の技術解説
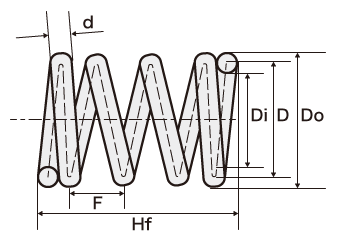



ばね各部の名称 ばね イチから学ぶ機械要素 キーエンス




3分で簡単 コイル と 磁界 の関係 向きや強さ 実用例を理系大学院卒ライターがわかりやすく解説 ページ 2 3 Study Z ドラゴン桜と学ぶwebマガジン




勉強しよう高校物理 コイルのインダクタンスの式
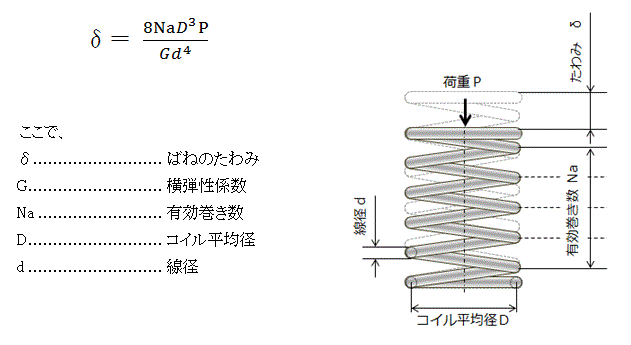



圧縮 引張コイルばねの計算方法




マナ物理 自己誘導 相互誘導1 解説 自己誘導 とは コイルに流れる電流が変化するとき コイル自身が作りだす磁場によって起電力が生じる現象 自己インダクタンス は コイルの巻き数 形状 内部の物質などで決まるコイル固有の
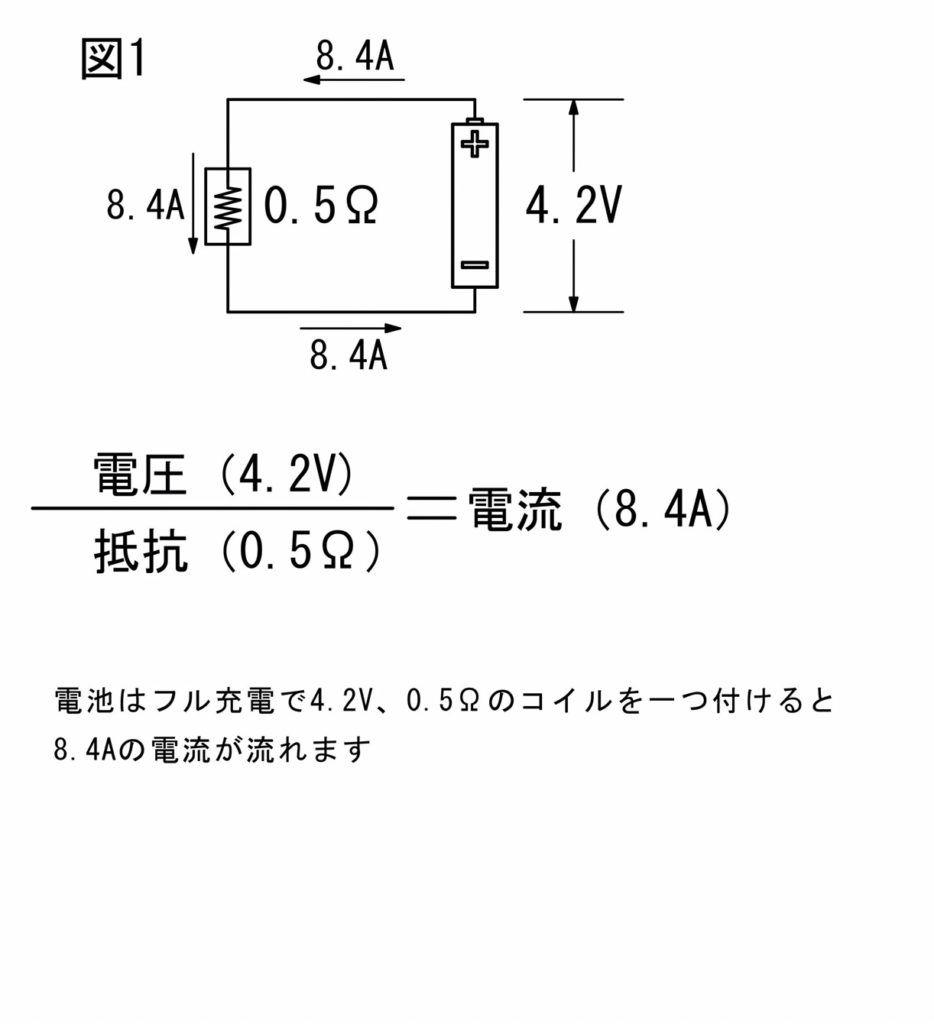



コイルの抵抗 ワイヤーの選定 巻き数の決定等々のお話 ベイホク店長岡野の場合 Vape北海道 公式サイト
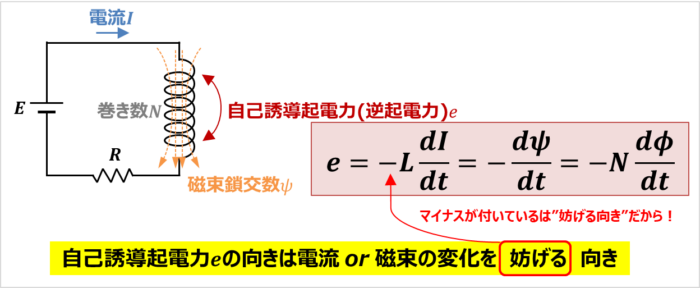



自己誘導のまとめ 公式 や 向き について解説



0 件のコメント:
コメントを投稿