で計算できちゃうんだ。 ガンガン問題をといていこう! そんじゃねー Ken1103 · ここでは、代表的な三角形の面積の公式 つを紹介します。 公式①底辺 × 高さ ÷ 2 まず つ目は、 底辺 と 高さ を使った最もオーソドックスな公式です。三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。
斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
不等辺三角形 辺の長さ 求め方
不等辺三角形 辺の長さ 求め方- · 三角形の成立条件について ABCの3辺をa,b,cとすると 三角形の成立条件は、(2辺の長さの和)>(残りの1辺の長さ)なので a+b>c a+c>b b+c>aというのはわかるのですが、 正確には答によると、a+b>cかつa+c>bかつb+c>a とあります。正弦定理から,三角形の辺の長さを求める計算について ABCにおいて a = 3 , A = 60°, B = 45°のとき b を求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわか


二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係
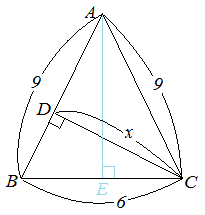
計算すると、 4 9 = c × c 13 = c × c よって、長い辺の長さは c = 13 (二乗して 13 になる正の数)となります。 では、 13 はどれくらいの長さでしょうか? 3 × 3 = 9 c × c = 13 4 × 4 = 16 なので、 13 は 3 より大きくて 4 より小さい数だと分かります。おかしな不等辺三角形 パラドックス 「不等辺三角形が二等辺三角形になる? 図1 と 図2 のように、AB>AC であるような不等辺三角形ABC の頂角A の二等分線と、底辺BC の垂直14 · 底辺と高さが決まれば面積も決まりますが 同じ面積で底辺以外の2辺の長さが異なる三角形は無数にあります よって、底辺と高さと面積がわかっていても 残り2辺の長さを求めることはで
· まとめ:直角二等辺三角形の辺の長さの求め方は2通りでクリア! 直角二等辺三角形の辺の公式はシンプル。 斜辺を求めるとき → √2をかける;0618 · 上野竜生です。三角形の辺や角が3つわかれば基本的に残りの3つも計算できます。その求め方をすべてのパターン網羅して考えます。 暗黙の了解 三角形abcにおいて∠aや∠b,∠cを単にa,b,cとし,aは辺bcの長さ,bは辺この三平方の定理では、斜辺^2 = 底辺^2 + 高さ^2 という換算式が成り立つのです。 つまり、斜辺の長さは底辺の2乗と高さの2乗を足し合わせ、ルート(√)をとったものといえます。
三角形の3つの辺がa = 3、b = 4、およびc = 5であるという問題が発生したとします。 三角形の半周長を計算します。 三角形の半周長を見つけるための方程式は次のとおりです。 S = a b c / 2。まず、三角形の3辺すべてを合計します。これは、a b cを意味し · 三角形において、 「2つの辺の長さa,bが分かっているとき、3つ目の辺の長さxは、 ab2 高さ (h) =SQRT (3)/2*B1 3 3辺の長さ (L) =3*B1 4 面積 (S) =SQRT (3)/4*B1^2


三角形 辺 の 長 さ


二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典
不等辺三角形角度求め方, 一般三角形の計算 数値を入力するだけで三角形の長さと、角度の計算を行ってくれるWebアプリケーションです。 一般三角形の計算 辺aか角Aの選択と数値の入力を行い、計算ボタンを押すと、その三角形の辺の長さと角度が表示されます。0417 · わたしの場合、決まった三辺の長さで三角形を書くとすれば まず一辺目の長さのlineを書き、 その線の両端を中心とした他の二辺と同じ半径の円を描いて 2つの円の交点と線の端点をスナップさせてlineと引く みたいに描きます。 外していたらごめんなさい。ブリタニカ国際大百科事典 小項目事典 二等辺三角形の用語解説 2つの辺が等しい三角形をいう。その等しい辺を等辺,第3の辺を底辺という。また2つの等辺によってつくられる角を頂角,2つの等辺の交点を頂点という。底辺の両端の角を底角といい,これら両底角は相等しい。


斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
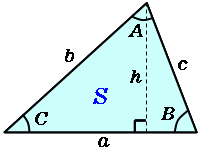


不等辺三角形 高精度計算サイト
1103 · 今までに習った「直角三角形」と「二等辺三角形」についてもきちんと理解しておきましょうね。 直角三角形とは?定義や定理、辺の長さの比、合同条件 二等辺三角形とは?定義や定理、角度・辺の長さ・面積の求め方 · 三角不等式は様々な「長さ」に拡張されています。→いろいろな三角不等式(絶対値,複素数,ベクトル) 三本の不等式を a a a について解くことで,条件を ∣ b − c ∣ < a < b c bc三角形の内心で辺の長さと比の値の求め方がわからないので 三角形の辺や角が与えられたとき残りの辺や角を求める方法 三角形の高さを求める 3つの方法 wikiHow;



直角三角形の辺を求める Youtube



簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
· この記事ではこんなことを紹介しています 三角形の面積を求めるための公式の一つに"ヘロンの公式"というものがあります。 この公式はどんなときに使えるのでしょうか? ここでは、ヘロンの公式が使える条件を説明したあと、実際に公式を使って三角形の面積を求める例題を示します。この数値はs = (abc)/2 で求められます。 三辺の長さがa = 4、b = 3、c = 5の場合s = (435)/2となり、s = (12)/2からs = 6になります。 ヘロンの公式の次の段階、A (面積)=sqr {s (sa) (sb) (sc)}を使用します(注:sqrはルートを意味します)。 Aには三角形の面積の公式をあてはめます。 つまり、1/2bh、1/2ah、または1/2chのどれを代入しても問題ありません。 計算をしてhを求めます。S = s ( s − a) ( s − b) ( s − c) ∗ s = ( a b c) 2



三角形 辺 の 長 さ


二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係
Step 1 で, b , A はわかりますが,もう1つの辺の長さ c はわかりません。そこで, c を求めるために,まずC = 180° A B より,C を求めます。 Step 2 Step 1で求めたCを用いて, つまり辺の長さ c を求めます。 これで,2辺 b , c とそのはさむ角 A がわかり余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます: a 2 =b 2 c 2 −2bc cos A この式をよく見ると、 「右辺は辺の長さだけ」 でできており、 左辺は角度だけ でできています。 したがって、この式を利用すると 「3辺の長さ」から、 「角 A 」 を求める ことができます。 (正確には、角 A そのものではなく cos A が求まりますが · 三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



簡単公式 二等辺三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
三角形の計算 ・ 正三角形 (辺から高さと面積) 正三角形の1辺の長さから高さと面積を計算します。 ・ 正三角形 (高さから辺と面積) 正三角形の高さから1辺の長さと面積を計算します。 ・ 正三角形 (面積から辺と高さ) 正三角形の面積から1辺の長さと高さを計算します。 ・ 直角三角形 (底辺と高さ) 直角三角形の底辺と高さから、斜辺と角度と面積を計算します直角三角形の3辺の長さの関係を表したものだよ その関係っていうのは、 $斜辺^2=底辺^2高さ^2$ だよ 辺の長さを求める時は、この式に当てはめることで求める 直角三角形辺の 長さ 求め方, 直角三角形 · 辺の長さが2桁でも気にすんな。 三平方の定理(ピタゴラスの定理)の公式にぶち込めばいいんだ。 x² = 5² 12² x = 13 直角三角形と言えども、いつも右下に直角が来るとは限らんぞ。



中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



3 おかしな不等辺三角形 Imujii S Page
不等辺三角形の選択した3つの入力値から他の要素の値を計算します。 入力指定 3辺abc 2辺abと高さ (Cは鋭角) 2辺abと高さ (Cは鈍角) 2辺bcと高さ (BとCが鋭角) 2辺bcと高さ (BかCが鈍角) 2辺abと夾角C 辺aと高さと角C 2角BCと夾辺a 2角BCと高さ 面積と2辺ab (Cは鋭角) 面積と2辺ab (Cは鈍角) 面積と2角BC 面積と辺aと角C 面積と高さと角C · 鋭角、直角、鈍角三角形における辺の長さの関係 というわけで 鋭角、直角、鈍角 それぞれのときに辺の長さにはどのような特徴があるかをまとめておきます。 直角三角形の場合 斜辺の長さの二乗が他の辺の二乗の和に 等しい でしたが 鋭角三角形の場合 一番大きい辺の長さの二乗は他の辺の二乗の和より 小さい 鈍角三角形の場合 · こんにちわ。 正弦定理と余弦定理を使えばいいのですが、コツがありますね。 ・向かい合う角と辺について、角の大きさと辺の長さがわかっているときには正弦定理を ・2辺の長さとそのはさむ角の大きさがわかっているときには余弦定理をあてはめればいいと思います。 たとえば、質問で書かれていた場合であれば、 >普通の三角形の一辺と2角が


このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋



三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく



直角二等辺三角形の辺の求め方 直角二等辺三角形の底辺が106センチメ 数学 教えて Goo



二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比
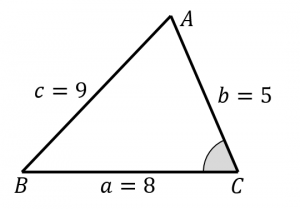


三角形の面積を3辺の長さから求める2つの方法 具体例で学ぶ数学


二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典


斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める



三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
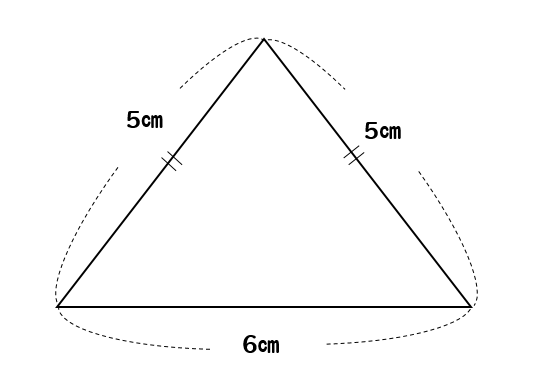


高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
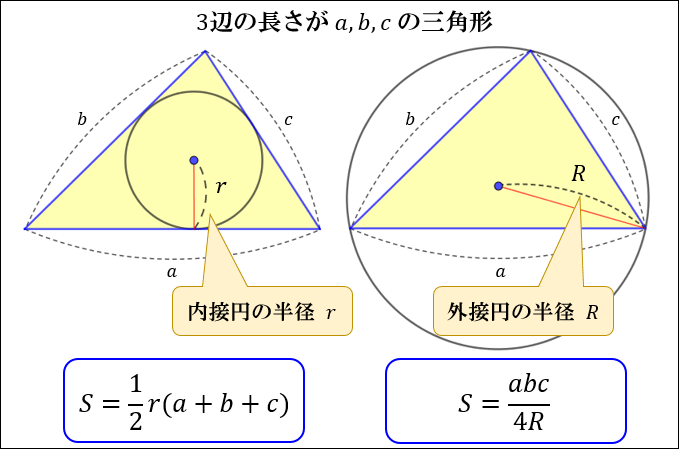


三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
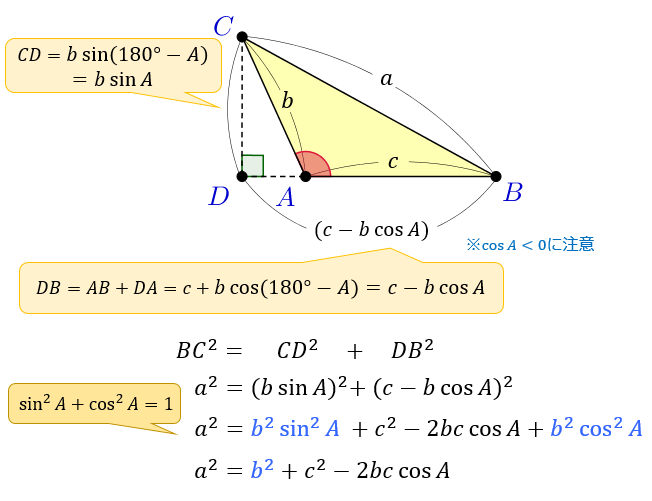


余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ



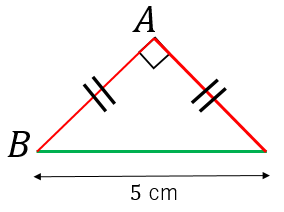
直角二等辺三角形 Wikipedia


直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明


このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋



正三角形面積計算 正三角形の公式 高さ 面積 Present Trek
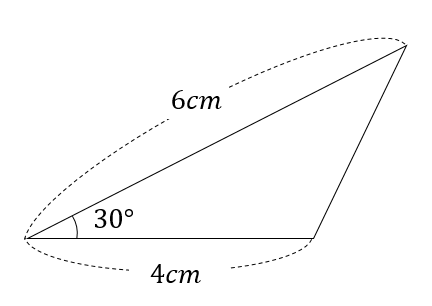


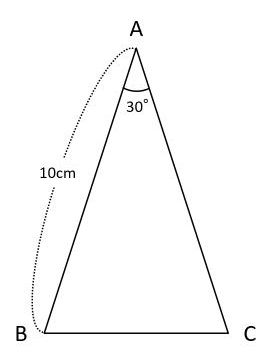
小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ


三角形 斜辺 長 さ 直角三角形
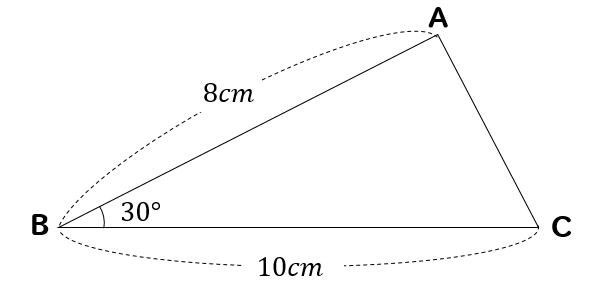


小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ



マイヤーズの三角形問題 テストの基礎 Qbookアカデミー



二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4


二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係



二等辺三角形 Wikipedia



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ


二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



不等辺三角形 至急ご回答お待ちしております 不等辺三角形について その他 学校 勉強 教えて Goo
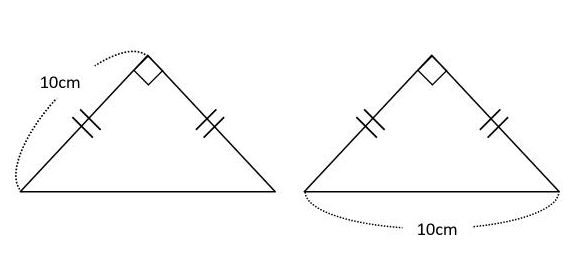


二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
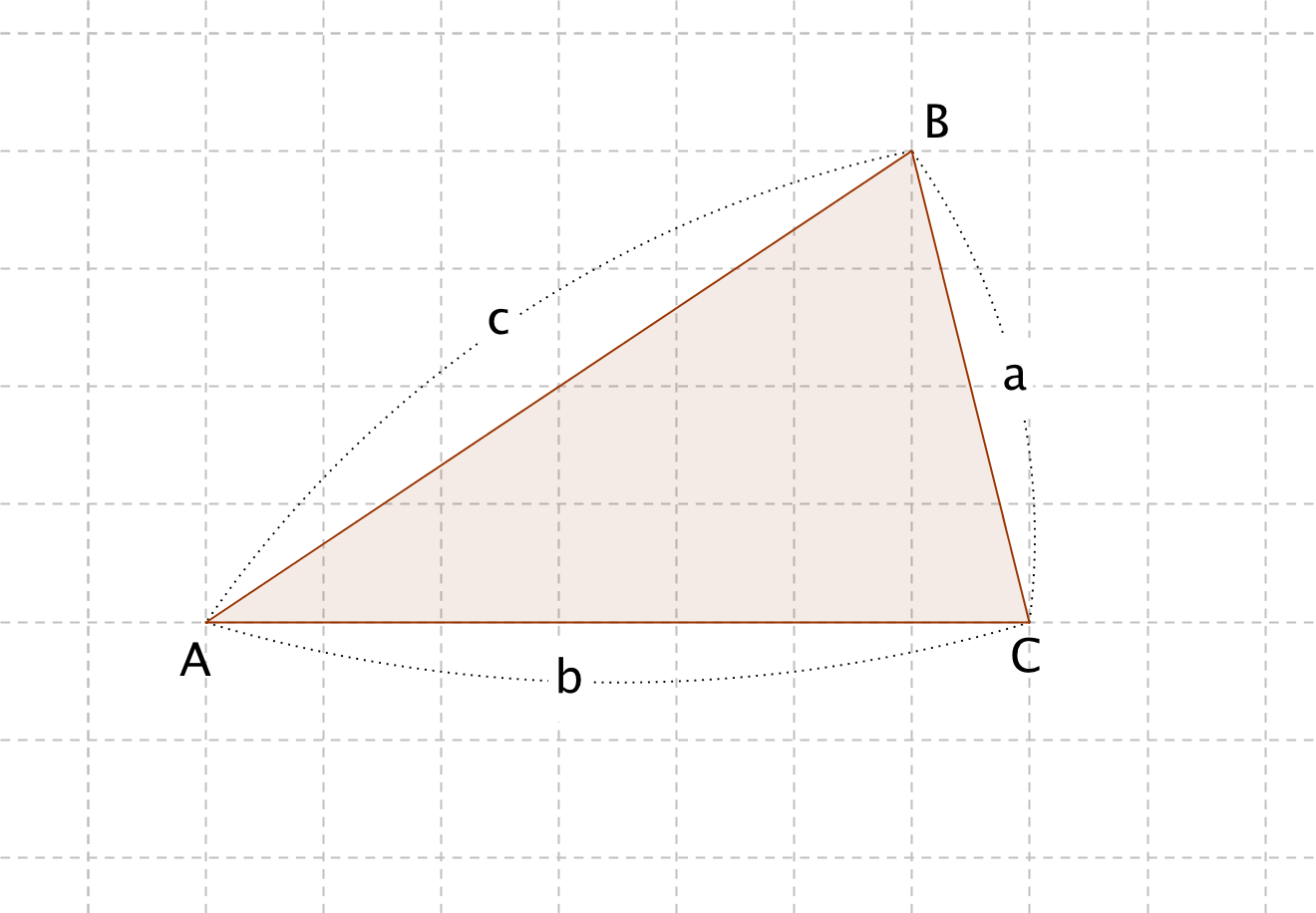


C言語入門 入力した3辺の長さから三角形の種類を判別 Webkaru


二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典


このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋


斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
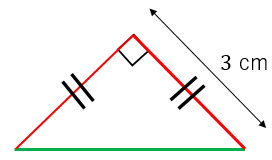


直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
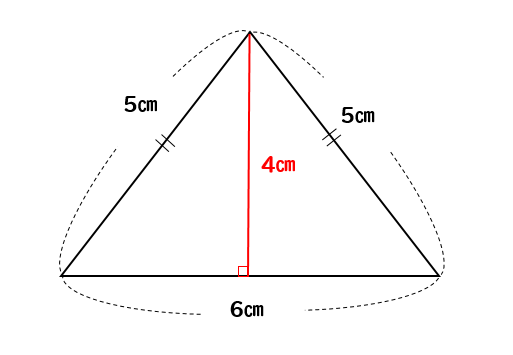


高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ


このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋



二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比



直角三角形 Wikipedia



二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
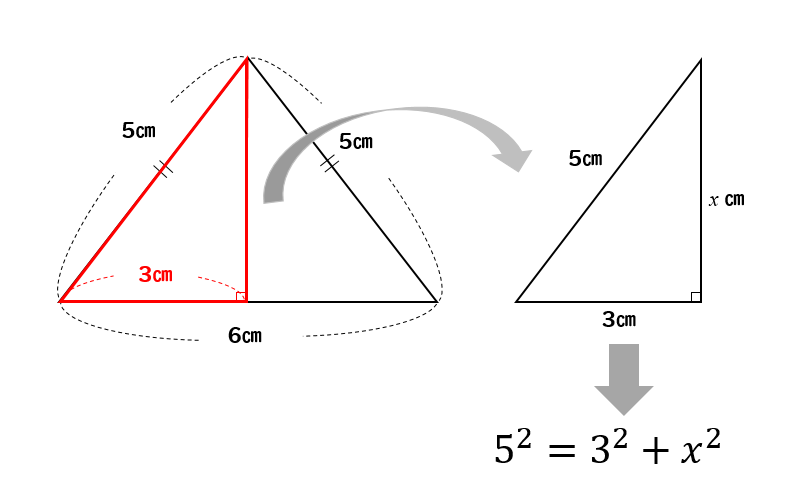


高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比



簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく



小5 算数 小5 42 三角形の面積 Youtube


プンチ ラマイ Montessori 三角形のお仕事



三角形 Wikipedia


外接円 外心について



最高 50 正三角形 面積 求め方



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ



名門国立小のカリスマ先生に聞く なんでこれがわからないの でイラっときた時の教え方 Forbes Japan フォーブス ジャパン
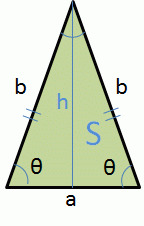


三角形の公式 Wakatta
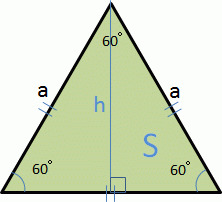


三角形の公式 Wakatta


不等辺三角形角度について教えて下さい 辺aが1367辺bが473 Yahoo 知恵袋


三平方の定理の応用



簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく


ヘロンの公式 計算機 三角形の面積と高さを 3辺の長さから計算します やまでら くみこ のレシピ


直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学


3 4 5の三角形で 本当に直角ができる Note Board
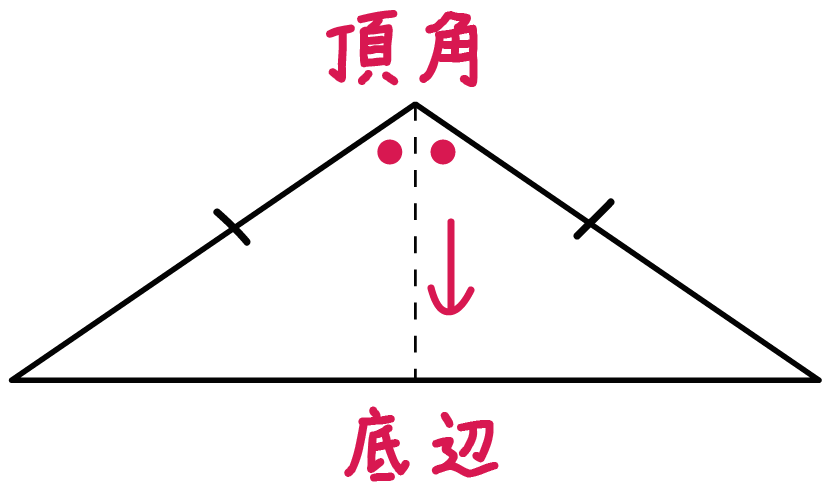


二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集


二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学


三角形 辺 の 長 さ



二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比



二等辺三角形の底辺の長さを弦 辺a 辺bの長さを弧とした場合の高さの 数学 教えて Goo


ヘロンの公式 不等辺三角形などの面積 角度 高さ 数学 エクセルマニア



簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく


二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく



頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo
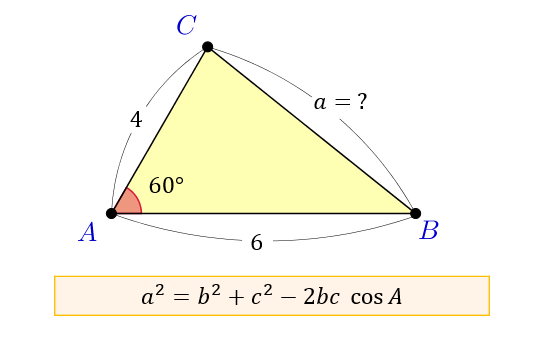


余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ


不等辺三角形や直角でない三角形の二辺の長さしか分かっていない場合どのよう Yahoo 知恵袋



不等辺三角形の定理 短編 あがた愛 ボーイズラブマンガ Kindleストア Amazon



必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



小学6年生で三角形の面積求め方わかりません 小学6年生の親です 学 数学 教えて Goo



二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



三角形 辺 の 長 さ



二等辺三角形の面積を求める算数の公式は


直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明
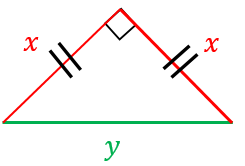


直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



号 テスト設計 技法 の必要性 Kouichi Akiyama Note
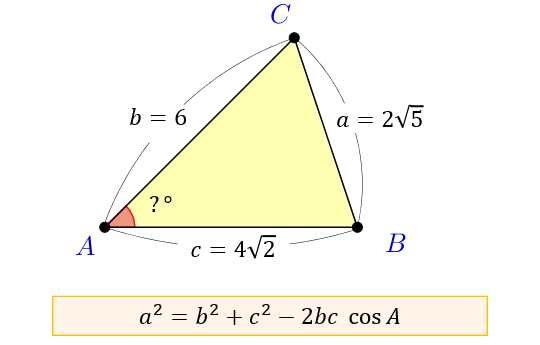


余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ



二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
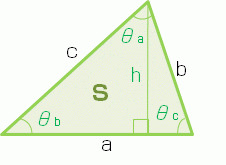


三角形の公式 Wakatta



0 件のコメント:
コメントを投稿